In the Math Module you define global variables and relations between them. They can be used in any mathematical text field for functions in graphs of any module of Shape.
Access to these variables and constants is given by a button labeled as Use global variables. Whenever this button is enabled, any variables with names defined in the Math Module will be replaced with the definitions in this module. A variable can be a function of previously defined variables and constants.
You can load and save presets for these from and into ascii files, allowing you to setup your own complex networks of constants and formula that you use frequently.
The basic procedure is to define constants and variables in the first column.
In the Expression column you either set a fixed value for a constant or define a mathematical expression from constants or variables defined further up.
The Value column then either repeats the value of the constant or computes the value of a more complex expression.
In the fourth column you can add a description of the constant or variable that you defined. |
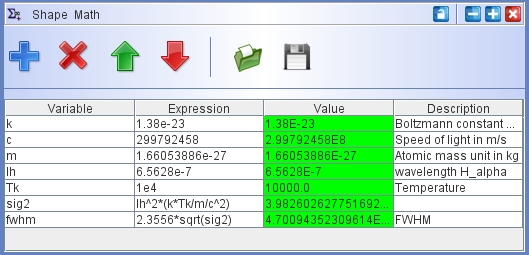
The setup in this screenshot of the math module is to define a Hα line in the Custom Species of the Physics Module. It first defines several physical constants, including the wavelength of Hα (lh), a temperature Tk and the resulting square of σ in the resulting gaussian line profile. The gaussian profile can then defined easily using the sig2 variable. The FWHM is also calculated as additional useful information.
|
Use the + and X buttons to add or delete variables, respectively. Since the order of the variables in the list may be important, you can move them up or down using the corresponding arrows buttons.
To save or load a set of variables to or from an ascii file, use the floppy disk or folder icon, respectively.
Units: Note that contrary to most of the astrophysics literature, in Shape we use Standard International (SI) units, i.e. MKS units based on meter, kilogram and seconds. For example, astronomers used to thinking in terms of particles per ccm should multiply all the densities by 1e6 before they put them into the density modifier. Unit conversions can be done easily on a number of websites nowadays, e.g. at UnitConversion.
Mathematical variables can have any letter+number string as names. Strings are separated by mathematical operators or spaces. Reserved strings include the most common trigonometric and logaritmic functions, e, pi, n (numerical density from the density modifier), and t (temperature from the temperature modifier).
When the letter e appears in numbers like 1e-2 it is interpreted as part of the number, yielding 100 for this case. When e is found as an individual string it is interpreted as the Euler number = 2.71828... Exponentials of this number are defined as e^c, rather than exp(c). |